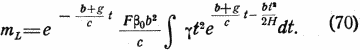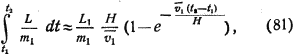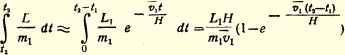1. Вертикальный подъем ракеты с людьми
Вертикальный подъем ракеты с людьми характерен тем, что благодаря присутствию людей опорное ускорение должно быть ограничено определенной максимально допустимой величиной. Нагрузка на поперечное сечение будет при этом достаточно значительной, так как речь идет о больших ракетах. Одновременно, согласно уравнению (31), скорость v должна быть очень большой; но так как допускаются лишь небольшие ускорения, то обычно она не может быть достигнута. Из уравнения (21) после его преобразования и интегрирования следует:
![]()
Желательно, чтобы большая часть топлива уходила на повышение скорости v и как можно меньше на преодоление сопротивления воздуха и силы тяжести. При вертикальном подъеме имеем:
![]()
На величину ∫gdt при вертикальном подъеме мы влиять не можем, так как ускорение силы тяжести g дано, а длительность полета t из-за наличия пассажиров невозможно сделать слишком короткой. Величина же ∫(L/m)dt будет тем меньшей, чем меньше L/m, т.е. чем выше нагрузка на поперечное сечение. Поэтому, хотя скорость v и не может быть достигнута, стремятся и здесь к наибольшей нагрузке на поперечное сечение.
Аналогичные рассуждения могут быть проведены и для наклонного подъема. Резюмируя, можно сказать: чем выше нагрузка на поперечное сечение, тем относительно меньше массы расходуется на преодоление сопротивления воздуха.
Большие ракеты могут стартовать и с поверхности моря, так как, если только отношение m/F велико, то и при большей плотности воздуха значение m/F : α, а тем самым и v0 достаточно велико.
Модель Е стартует, следовательно, при наиболее высоком допустимом опорном ускорении. Величина α будет при этом постоянной в течение всего времени работы двигателя.
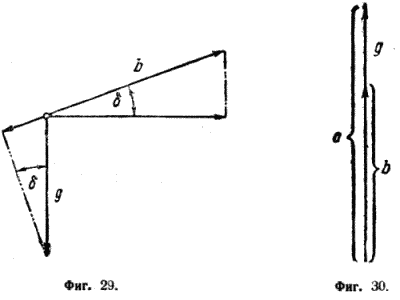
Если ускорение b образует с горизонталью угол δ (фиг. 29), то
b + g sin δ = α;
При вертикальном подъеме (фиг. 30) sin δ = 1, и мы получим:
b = a - g (62)
Таким образом действительное ускорение в пределах атмосферы можно считать постоянным, а идеальное ускорение
bx = a + L/m (63)
будет переменной величиной, так как ускорение ограничивается не свойствами аппарата или величиной тяги, а лишь учетом свойств человеческого организма. Если L увеличивается, то одновременно следует увеличивать и Р, для того чтобы опорное ускорение не изменилось.
Подъем в атмосфере
В связи с незначительным ускорением модель Е должна пройти большой путь для получения полной скорости. При этом в атмосфере ускорение силы тяжести g можно с достаточным приближением считать постоянным. В случае вертикального подъема величина b также постоянна, и мы получаем.
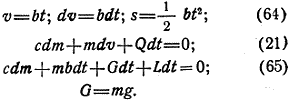
Согласно (27)
L = Fγβv²
Принимая во внимание (34) и (64), получим:
![]()
Если подставить (66) в (65), оно примет такой вид:
![]()
Это линейное дифференциальное уравнение относительно m и t. Отсюда следует:
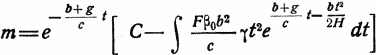
Постоянная интегрирования С определяется из условия t = 0. Тогда С = m0, и таким образом
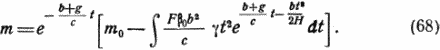
Изменение факторов, обусловливающих сопротивление воздуха, влияет лишь на подинтегральное выражение. Последнее показывает, следовательно, расход массы из-за сопротивления воздуха, т.е. характеризует влияние сопротивления на конечную массу поднятой и получившей ускорение ракеты.
Если обозначить через mL расход массы, обусловленный сопротивлением воздуха, то из (68) получим:
|
| Здесь также входит величина |
|
Это станет понятным, если учесть, что сопротивление воздуха противодействует относительно сильнее пустой ракете, чем полной, и что вся формула имеет в своей основе закон импульсов.
Величина m0 не входит в формулу (70). Это также понятно. Расход топлива на преодоление сопротивления воздуха влияет на величину массы ракеты, но зависит лишь от величины, формы ракеты и скорости полета, а не от начальной массы и удельного веса.
Влияние сопротивления воздуха на расход массы определится, если поделить выражение (68) на равенство
![]()
которое получается из (68), если пренебречь сопротивлением воздуха, т.е. если принять, что β0 или γ равны нулю. Тогда
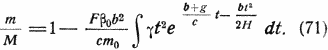
Отсюда можно заключить, что m останется положительной (это значит, что ракета проникнет сквозь атмосферу) только в том случае, когда второй член правой части уравнения будет меньше единицы, т.е. когда
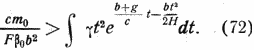
Таким образом необходимо выбирать с и m0 возможно большими, a F — возможно малым. В отношении β0 выбор вряд ли возможен, большим ракетам придется стартовать с водной поверхности, т.е. в большинстве случаев с поверхности моря.
Как видно из формулы, уменьшение ускорения b влияет, по крайней мере в начальный момент, благоприятно на сопротивление воздуха. Этим выражается лишь то, что сопротивление воздуха тем меньше, чем медленнее летит ракета. В дальнейшем, однако, при увеличении пределов интегрирования начальное благоприятное влияние прекращается, так как, чем медленнее летит ракета, тем больше сказывается вредное действие силы тяжести. Но совершенно независимо от этого, мы будем принимать ускорение b настолько большим (не достигая наивыгоднейшей скорости), насколько это допустимо с точки зрения воздействия на человеческий организм.
Наряду с расходом на преодоление сопротивления воздуха масса расходуется также и на преодоление силы тяжести; при вертикальном подъеме модели Е на преодоление силы тяжести расходуется больше массы, чем на преодоление сопротивления воздуха. Сопротивление воздуха в начале полета благодаря небольшой скорости полета невелико, затем оно увеличивается, под конец опять уменьшается и, наконец, перестает действовать совсем. Максимум значения сопротивления воздуха LH и можно определить, если продифференцировать L no t или, еще лучше, ln L по t [см. (66)], так как, если L имеет максимум, то и ln L будет его иметь:
![]()
Максимальное значение L (мы его обозначаем через LH) будет получено обычным путем. Приняв γ = const, будем иметь
![]()
откуда следует:
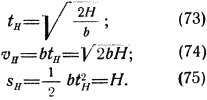
Полученные величины интересуют нас постольку, поскольку на этой высоте ракета с человеком претерпевает наибольший риск быть раздавленной сопротивлением воздуха. Внутреннее давление в ее резервуарах должно быть таким, чтобы выдержать действие сопротивления воздуха. Если они выдержат на этой высоте, то они выдержат на всей траектории полета*.
Так как желательно, чтобы резервуары в ракете, работающей на водороде, находились под слабым давлением, а их стенки были возможно тонкими, то необходимо, чтобы такая ракета помещалась в герметически закрывающейся толстостенной оболочке, которая раскрывается лишь тогда, когда горючее ракеты, работающей на спирте, израсходовано и сопротивление воздуха уменьшилось.
Для H = 7300 м и b = 30 м/сек² находим tH = 22,0 сек. и vH = 661 м/сек. Сила сопротивления воздуха составит здесь (γ принято 1/24)
LH = 6690 кг/м² = 0,669 кг/см²
Замедление, т.е. потерю скорости из-за сопротивления воздуха, мы найдем, если силу сопротивления L поделим на массу ракеты, или, что то же, силу сопротивления воздуха, приходящуюся на 1 см² поперечного сечения, поделим ка нагрузку на поперечное сечение и частное от деления умножим на 9,81 (нагрузка на поперечное сечение модели Е будет на этой высоте 0,925). Замедление, таким образом, равно:
![]()
В ближайшие секунды после этого замедление будет еще несколько большим, так как знаменатель m дроби L/m уменьшается все время, между тем как числитель L вблизи своего максимума можно с известным приближением считать постоянным. Максимум замедления будет при
![]()
(При конструировании необходимо следить за тем, чтобы к этому времени t было L/m ≤ g) Непосредственное вычисление этой величины настолько сложно и требует так много труда, что ее нецелесообразно здесь уточнять. В правильности формулы (76) для каждого конкретного случая можно убедиться, если составить таблицу или диаграмму относительного замедления для вертикального подъема ракеты с пассажирами.
При подсчете выражения
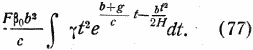
необходимо установить зависимость γ от v, т.е. от bt. Однако сейчас об этом рано говорить, ибо пройдет еще много лет до старта модели Е, и, кроме того, точное значение γ можно будет установить лишь после подъема.
Как показал Роте, кривая значений γ не имеет одинаковой формы для всех снарядов, и можно ожидать, что модель Е при ее габаритах и ее больших стабилизирующих поверхностях будет иметь другие коэффициенты сопротивления, чем аналогичные по форме артиллерийские снаряды. Если известен точный вид кривой сопротивления, то по ней можно построить функцию v, которая даст γ с достаточным приближением. Интерполяция должна давать особенно точное соответствие при v = 800 м/сек, потому что в этой области относительное замедление от сопротивления воздуха является наибольшим [ср. (76)]. Кроме того, необходимо стремиться, чтобы при назначении этой функции ее аналитическое выражение допускало интегрирование в элементарных функциях (если интегрирование не проводится графически, что здесь особенно желательно).
В своих расчетах мы принимаем, что в пределах 0 — 300 м/сек и свыше 460 м/сек величина γ постоянна. Затем вводим новую переменную
![]()
и приводим интеграл (77) к такой форме:
![]()
Это выражение может быть представлено в виде
![]()
Здесь буквами А — G обозначены постоянные. Интеграл не берется в элементарных функциях, но легко разлагается в хорошо сходящийся степенной ряд, а для x > 1 может быть сведен к еще быстрее сходящимся интегралам
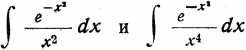
Действительно,
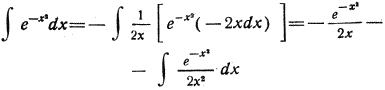
и дальше:
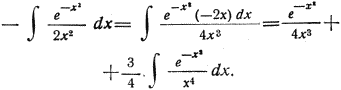
В интервале значений от 300 до 400 м/сек можно принять изменение значений γ по параболе третьего порядка вида H + Ix + Kx² + Lx³ для которой интегрирование выполняется аналогично приведенному Этим путем находим, что потеря скорости от сопротивления воздуха составит
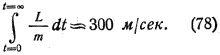
В случае вертикального подъема модели Е необходимо, чтобы идеальная скорость vx была на 300 м/сек больше, чем в случае полета в совершенно разреженной атмосфере или при бесконечно тяжелой ракете.
В формуле (68) было сделано предположение, что величины b и g имеют постоянные значения, но в действительности только сумма b + g = a является постоянной, в то время как
![]()
Однако для расчета подъема в области земной атмосферы такой точности не требуется, так как формулой (68) приходится пользоваться лишь для высот до 150 км. При больших высотах сопротивлением воздуха можно пренебречь и, следовательно, применять значительно более простые формулы. На высоте 150 км над поверхностью земли ускорение силы тяжести g = 0,95 g0. Так как сила тяжести на подъеме до этой высоты приводит к потере скорости в 100 м/сек, то, приняв g = g0. получим ошибку меньше, чем 0,5·100=5 м/сек. Если же пользоваться средним значением g, то ошибка будет исключительно мала, и, например, при gm = 0,98 g0, она станет меньше 1 м/сек.
Совсем другое получится, если при вертикальном подъеме ракеты принимать g постоянными до того момента, когда скорость ракеты станет параболической*. Здесь ошибка может оказаться порядка 1 км/сек. В этом случае необходимо учитывать изменение силы тяжести. Задача эта решается, но результаты имеют только теоретический интерес, так как в ближайшей главе будет показано, что для ракеты с пассажирами вертикальный подъем не является наилучшим и что с наименьшей потерей энергии она пролетит, если во время работы двигателя полет ее будет совершаться параллельно воздушному океану. Так как формулы, учитывающие переменное значение g при вертикальном подъеме, достаточно сложны, можно ограничиться здесь установлением границ, в которых может колебаться величина потери скорости из-за влияния силы тяжести.
Таким образом ставится задача о сообщении ракете параболической скорости. Делаем упрощающее предположение, что g — постоянно. Тогда и ускорение постоянно (b = a — g).
Если обозначить через vp параболическую скорость, через r —радиус Земли и через s — путь, на котором должен работать двигатель ракеты, чтобы она получила параболическую скорость, то из формул (57), (60) и (58) получим:
![]()
Затем для равноускоренного движения (при постоянном b)
![]()
Сравнивая обе величины, получим:
![]()
Принимаем, что за все время работы двигателя g = g0 = 10 м/сек². Тогда из (80) получаем:
s = 1 970 км; vp = 9 850 м/сек.
В этом случае идеальная скорость была бы
![]()
Так как при достижении параболической скорости ускорение силы тяжести составит только 5,75 м/сек², то, принимая опорное ускорение 35 м/сек², получим фактическое ускорение b в последнюю секунду полета равным 29,25 м/сек². Если бы в расчетах принять это значение ускорения, то получилось бы
vp = 10 040 м/сек
Если же при определении потери скорости под действием силы тяжести исходить из этого малого значения g, то
![]()
Таким образом при опорном ускорении, равном 35 м/сек²,
12 300 м/сек < vx < 14 080 м/сек.
При этом значение идеальной скорости лежит не в середине между этими пределами, а существенно ближе к высшему пределу (около 13 700 м/сек), так как ракета во время подъема большую часть времени находится под влиянием более сильного поля тяжести.
При опорном ускорении 40 м/сек² получим:
12 720 м/сек < vx < 13 630 м/сек.
При опорном ускорении (гипотетическом) 70 м/сек² получим:
12 300 м/сек < vx < 12 500 м/сек.
Разницей между скоростью по отношению к центру Земли и скоростью по отношению к земной поверхности здесь пренебрегаем.
2. Влияние сопротивления воздуха на свободный полет регистрирующих и далеко летающих ракет
Вертикальный подъем
Работа двигателей этих ракет, как правило, прекращается, когда они еще находятся в пределах земной атмосферы. Скорость по отношению к окружающему воздуху в момент прекращения работы двигателя обозначим через v1, а через L1 и β1 — сопротивление воздуха и давление в этой точке траектории. Через t2 — t1 сек. скорость будет v2, сопротивление воздуха L2 и давление воздуха β2. Тогда
Имея в виду, что в атмосфере с заметным сопротивлением воздуха v изменяется весьма мало, можно также написать:
Замедление из-за сопротивления воздуха составит
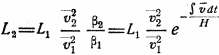
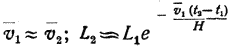
|
* |
а полное замедление
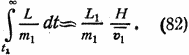
Если v1 будет оптимальной скоростью в точке s1 то L1/m1 = g и полное замедление равно (H/v1)·g. В случае, если скорость vn будет меньше v1, то полное замедление из-за сопротивления воздуха будет соответственно меньше:
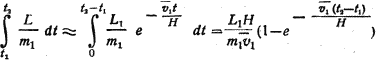
т.е. в vn/v1 раз меньше
Для случая v1 = 1000 м/сек и при соответствующих других величинах получается, например,
![]()
(точнее 69 м/сек; разница так мала отчасти потому, что различные неточности, которые допускались, погасили друг друга). Для v1 = 10 000 м/сек отношение L1/m1 = 3 м/сек² (здесь s больше, а поэтому и H, а следовательно, и содержание водорода в воздухе больше*), полное замедление составляет 2,2 м/сек, т.е. исчезающе малую величину.
Наклонный подъем ракеты
В этом случае интергал ∫L/m1dt следует поделить на синус угла наклона траектории δ в момент окончания работы двигателя. Мы выбираем угол наклона траектории к горизонту в начальный момент перехода на полет по инерции по тем же соображениям, по которым мы пришли к выводу, что Q должно быть верным в начале полета.
При повторном вступлении ракетного снаряда в область земной атмосферы расчет сопротивления воздуха следует производить так же, как и для артиллерийских снарядов, пользуясь методами балистики.
Следует вкратце остановиться на вопросах приземления ракет дальнего действия, снабженных парашютами. (Эти расчеты непригодны для рассмотрения полета межпланетных ракет, входящих в атмосферу горизонтально со скоростью, большей круговой *.)
Они вступают в воздушную атмосферу со скоростью 2 — 7 км/сек и под углом αopt, подсчитанным для этой скорости по формуле (0) предыдущей главы. Парашют раскрывается и ракета приземляется со скоростью ve.
О последнем участке полета достаточно сказать несколько слов. Скорость здесь определяется тем, что сопротивление воздуха равно весу.
По (27) получим:
F·γ·β·ve² = m1·g (a)
(обозначения те же, что и в гл. V).
На больших высотах ve благодаря меньшему сопротивлению воздуха имеет большее значение:
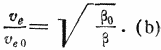
Более подробно необходимо рассмотреть участок траектории, на котором происходит торможение, причем расчеты можно значительно упростить, не принимая во внимание в первом приближении ускорение силы тяжести g. Вначале ракета ведет себя примерно так, как тело, предоставленное самому себе в мировом пространстве, и изменение скорости благодаря силе тяжести в течение этого короткого времени не имеет существенного значения по сравнению со скоростью порядка нескольких км/сек. В дальнейшем опорное ускорение становится настолько большим, что по сравнению с ним силою тяжести можно пренебречь, тем более, что в это время опорное ускорение определяется лишь сопротивлением воздуха. Только для конца периода торможения такие методы расчета теоретически недопустимы; однако эта часть траектории полета нас в дальнейших исследованиях не интересует. Кроме того, упростить расчеты можно тем, что рассматриваемый нами короткий участок будем считать прямолинейным.
Определяем замедление:
![]()
Здесь β0 — плотность воздуха на поверхности земли, а остальные обозначения — те же, что и в гл. V.
Дальше имеем [см. (34)]:
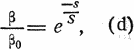
где
s — отрезок прямолинейной траектории полета ракеты, продолженный до поверхности земли;
S — расстояние, которое должна пройти ракета, чтобы сопротивление воздуха увеличилось в е раз.
Далее,
ds = - vdt
Умножением равенства (с) на dt/v и с учетом (d) и (е) получим:
![]()
откуда после интегрирования с использованием (d) получим:
![]()
Здесь v0 — скорость вне атмосферы, v — скорость в исследуемой точке траектории, β1 — давление воздуха вне атмосферы (естественно, равное нулю).
В конечном итоге получаем:
![]()
Если принять во внимание (с) и (е), то замедление составит
![]()
Значение vdv определяем из (g):
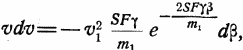
в то время как из (d)
![]()
следовательно,
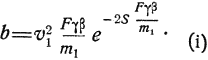
Таким образом можно легко подсчитать b (изменение значений b см. на фиг. 36,с).
Как только будет найдена зависимость между путем, скоростью и ускорением, вычисление остальных величин, входящих в формулы, не представит особых трудностей*.
К сожалению, чтобы не перегружать книгу, мы не можем на этом остановиться более подробно.
Необходимо лишь рассмотреть максимальное значение замедления, для того чтобы установить прочность строп парашюта и величину опорного ускорения, которому подвергается груз.
Плотность воздуха, при которой опорное ускорение будет максимальным, может быть найдена, если продифференцировать b по β из (i):
![]()
Если это значение подставить в (i), то получим максимальную величину замедления
![]()
Интересно отметить, что F, γ и m1 не входят в выражение для bmax.
Необходимо еще заметить, что мы приняли простой парашют, у которого (Fγ)/m1 остается постоянным. Кривая значений b будет, однако, совершенно иной, если снабдить парашют предохранительными клапанами, которые откроются, когда разность давлений между внешней и внутренней сторонами будет слишком большой (см. фиг. 36,b).
Согласно гл. V, S = H cosecα, если через α обозначить угол между траекторией и горизонтом. Для регистрирующей ракеты, поднимающейся, например, вертикально вверх, α = 90°
и
![]()
что при v1 = 1ООО м/сёк составит 25,8 м/сек², или 2,6 ускорений силы тяжести.
Ракеты дальнего действия лучше всего поднимаются вверх под углом, определяемым по формуле (о) гл. VII. Само собой понятно, что под этим же углом они возвращаются опять в атмосферу. Из формулы (о) гл. VII следует
![]()
где х определяется из формулы (а) гл. VII:
![]()
Тогда
![]()
Для дальности полета 1000 км v1 = 3160 м/сек и bmax составит 18 ускорений силы тяжести; для дальности 2000 км bmax будет больше примерно в 2 раза, т.е. составит 36 ускорений силы тяжести.
Для того чтобы определить наибольшее bx, которое может наступить в наиболее неблагоприятных условиях, а также соответствующие ему величины дальности полета и конечной скорости, необходимо в формуле (n) продифференцировать b по x. Подсчет намеченных здесь экстремальных значений легче провести, если дифференцировать не саму величину b, а ее логарифм ln b.
Для
![]()
получим
x = 0,74926
Соответственно конечная скорость составит по формуле (а) гл. VII v1 = 6830 м/сек и дальность полета — 8150 км. Замедление достигнет при этом 53,5 ускорения силы тяжести.
Ракета весом 50 кг нагрузит в этом случае стропы парашюта силой 50·53,5 = 2675 кг.
При этом необходимо принять во внимание, что при помощи упомянутых уже выше парашютных клапанов возможно снизить максимальную величину опорного ускорения до четверти подсчитанного здесь значения.
Принцип действия парашютных клапанов заключается в следующем. Парашют не допускает, чтобы сопротивление воздуха было больше, чем, например, b2m1. Как только оно начинает превышать эту величину, воздух открывает клапаны парашюта и частично проходит через них так, что сила торможения этим соответственно уменьшается. Таким образом торможение остается так долго постоянным и равным b2, пока вследствие продолжающегося уменьшения скорости получится, что
![]()
Это может наступить, если скорость уменьшилась, например, до v3. Пока работают клапаны парашюта, скорость благодаря постоянному замедлению равна
v = v2 - b2t (o)
Путь, пройденный ракетой за время действия клапанов,
![]()
и соответственно плотность воздуха составит
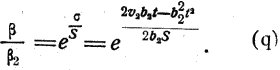
Значение β2 может быть получено из формулы (i) графическим путем или подбором, так как остальные величины входящие в формулу, даны. Если получено значение β2 можно вычислить v2
![]()
Вообразим себе ракету с простым парашютом. Пусть массы реальной и воображаемой ракет будут одинаковыми и парашют реальной ракеты будет при закрытых клапанах иметь ту же тормозящую силу, что и парашют воображаемой ракеты. И, наконец, пусть эта воображаемая ракета летит возле реальной с той же скоростью. Сопротивление воздуха для воображаемой ракеты составит
L1 = Fγβv²
После некоторых преобразований, принимая во внимание формулу (q), получим:
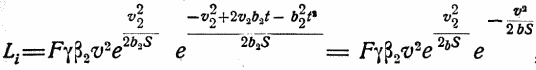
или при учете формулы (r)
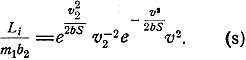
Точка, где клапаны опять закроются, может быть определена, исходя из того, что здесь Li должно быть равно реальному сопротивлению воздуха.
Таким образом в этом месте
![]()
Эта точка может быть лучше всего найдена графически. Положим, хотя бы
![]()
достроим кривую
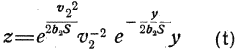
и на кривой найдем место, где z = l.
Известный интерес представляет также вопрос о том, когда эти клапаны при определенной скорости и определенном, еще допускаемом максимальном замедлении b2 используются наиболее эффективно. Это будет, очевидно, тогда, когда Li достигнет максимума по сравнению с наивысшим допускаемым cопротивлением воздуха.
Из формулы (t) следует:
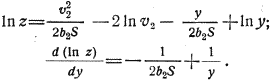
Это выражение, очевидно, будет равно нулю, если
y = v² = 2·b2·S
После того как скорость достигнет значения v3, клапаны закроются и парашют будет опять действовать, как обычная Конструкция. В дальнейших расчетах будем соответственно исходить из формулы (f), принимая для начальных значений скорости и давления воздуха величины v3 и β3.
Тогда
3. О полете реактивных самолетов в атмосфере
Под реактивными самолетами мы понимаем самолеты, которые вместо воздушных винтов снабжены реактивными двигателями. Как было указано в гл. VII,
P = R + Q (84)
где Р — суммарная реактивная сила, Q — сила, требующаяся для поддержания самолета и для преодоления сопротивления воздуха, R — сила, придающая самолету ускорение. Q может быть определено из формул (26) и (27):
где k — отношение лобового сопротивления к подъемной силе*; δ — угол подъема траектории относительно горизонта.
Формулы для подъема ракеты с оптимальной скоростью были приведены нами в гл. V и там же было показано, что ракета используется наилучшим образом, если поднимается вертикально. Но, как будет показано в последующих главах, некоторые обстоятельства могут привести к тому, что при наклонном подъеме все же будет экономиться топливо.
Вследствие действия опорного ускорения на организм человека самолеты с людьми не смогут лететь с оптимальной скоростью и потери на преодоление сопротивления воздуха и силы тяжести будут всегда наименьшими при вертикальном подъеме. Если принять δ ≠ 90°, то
При этом мы еще не учли потерь на трение о несущие поверхности, которых нет у обычных ракет. Таким образом можно притти к выводу, что наклонный полет ракеты с несущими поверхностями не сможет облегчить задачу проникновения в межпланетное пространство.
При спуске несущие поверхности могут значительно увеличить дальность. Если, например, ракета дальнего действия без них спускается под углом 45° со скоростью 2 км/сек, то, согласно гл. VII, она пройдет расстояние 400 км. Если же эта ракета летит горизонтально и спуск происходит с высоты 50 км, причем она снабжена несущими поверхностями, то дальность, достигает 1350 км (подробнее об этом см. гл. XV).
4. Наклонный подъем модели Е по прямой
Представим себе ракету для межпланетных путешествий-(см. фиг. 13, 29 и 44), которая поднимается по прямой, наклоненной под углом α к горизонту. Ось ракеты должна при этом быть направлена несколько более круто, с тем чтобы тяга и аэродинамическая подъемная сила уравновесили силу тяжести; в противном случае направление полета будет постепенно изменяться.
В безвоздушном пространстве ось ракеты должна была быг образовать сравнительно большой угол с направлением полета,, а в нижних слоях атмосферы благодаря возникающей аэродинамической подъемной силе этот угол может быть значительно меньшим. Пусть угол между осью и горизонтом равен β.
Как известно
Q = L + gm·sin β
Из аналогии с выводами формул (61)—(68) следует:
![]()
![]()
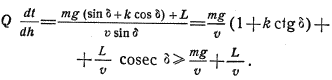
|
* |
В данном случае имеем*
b + g·sin β = α; L = F·γ·β·v²
Если обозначить через y высоту над поверхностью земли и чеоез s — пройденный путь, то получим:
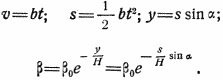
Из этих выражений следует:
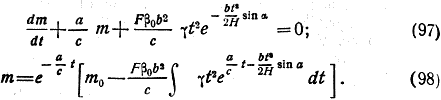
Интересно, что при наклонном подъеме, если только он происходит по прямой, сопротивление воздуха достигает наибольшего значения на высоте Н км, в то время как относительное замедление достигает высшего значения на высоте, большей на 3—5 км.
Если же ракета поднимается по кривой, то, пользуясь формулой (96), следует составить уравнение
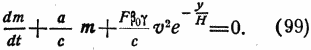
После интегрирования этого уравнения получим:
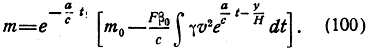
При вычислении интеграла необходимо, конечно, выразить v, t и y через заданный аргумент.